Fibre Tapping and New Advances in MCDA

The Phoenix LSP2 is currently being organised by PPC S.A. Greece. Hydroelectric Power Plants (HPP’s) participating in LSP2 communicate via optical fibres. We review briefly the possibility of eavesdropping on optical fibres, a process known as fibre tapping. Moreover we report on some recent advances on MCDA algorithms which are a key ingredient in Phoenix.

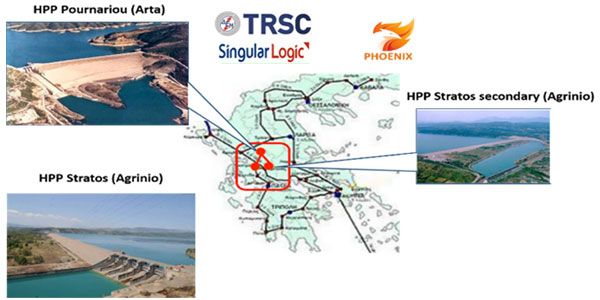
PPC S.A. Greece is organising the Phoenix Large Scale Pilot 2 (LSP2) in WP7 which will feature 2 Main Hydroelectric Power Plants (MHPP) plus 2 secondary ones (SHPP) attached to the main ones. Both MHPPs have an earthen dam. MHPP Pournari 1 is located near the city of Arta in the Mid-West part of Greece and has an installed power capacity of 300 MW. SHPP Pournari 2 is located 2.5 km from Pournari 1, shares the same water tank  and has an installed power capacity of 33.6 MW. MHPP Stratos 1 is located near the city of Agrinio again in the Mid-West part of Greece and has an installed power capacity of 150 MW. SHPP Stratos 2 is located 3km from Stratos 1, shares the same water tank and it has an installed power capacity of 6.3 MW. In both cases the MHPPs communicate with the corresponding SHPPs via optical fibres. A key issue then is whether one could eavesdrop on optical fibres, a process known as “fibre tapping” (FT for short).

Let’s remind ourselves that in mobile networks information (data) is transmitted using radio frequencies (RF) whereas in optical fibres information (data) is transmitted using visible light (VL), both RF and VL are electromagnetic waves although of different frequencies: in mobile networks the following frequencies are used –all generations (400-5000 MHz) whereas visible light frequency spectrum  is 400-800 THz. In principle, FT is possible although it is more difficult to perform than eavesdropping on RF communications (see for example [1] for a brief exposition and especially  [2] for a detailed exposition).

How could one eavesdrop on optical fibres then?

Well, first one has to peal-off the plastic cover of the optical fibre to expose the glass.

Second, simply bend the optical fibre to extract the light out of it and then apply a photodiode and turn light into electric current.

OR

Apply optical splitting. This method causes some disruption on the line, as the optical cable is split using a clip that cuts into the cable and attaches a second fibre cable, which transmits light from the main fibre to a device controlled by the attacker.

What are the possible countermeasures against FT?

The first method is to apply a fibre optic sensor and monitor attenuation along the fibre.

Attenuation in fibre optics, also known as transmission loss, is the reduction in intensity of the light beam (or signal) with respect to the distance travelled through a transmission medium. Attenuation coefficients in fiber optics usually use units of dB/km through the medium due to the relatively high quality of transparency of modern optical transmission media. The medium is typically a fiber of silica glass that confines the incident light beam to the inside. Attenuation is an important factor limiting the transmission of a digital signal across large distances. Thus, much research has gone into both limiting the attenuation and maximizing the amplification of the optical signal. Empirical research has shown that attenuation in optical fibers is caused primarily by both scattering and absorption

Attenuation (denoted A, measured in dB) in fiber optics can be quantified using the following equation (W denotes Watts):

A (dB) = 10 X log ₁₀ [Input Intensity (W) / Output Intensity (W)]

The second method is to apply optical interferometry techniques to monitor the speckle pattern of the system: A modally dispersive coherent light traveling through the multi-mode fibre mixes at the fibre’s terminus, thus resulting in a characteristic pattern of light and dark splotches called “speckle pattern”. The laser speckle is stable as long as the fibre remains immobile, but flickers when the fibre is vibrated. A fibre-optic sensor works by measuring the time dependence of this speckle pattern and applying digital signal processing to the fast Fourier transform (FFT) of the temporal data.

The third method is (classical) cryptography and especially quantum cryptography (see for example [3]).

Modern classical cryptography-mathematically speaking- is mainly based on factoring out large integers into a product of primes, this is a “hard problem” in complexity theory. There are various algorithms achieving this. On the other hand, quantum cryptography is based on Bell’s inequalities (Bell’s theorem, CERN, 1964) in quantum mechanics which imply “No Quantum Xeroxing”. The later implies that no eavesdropping is possible in the public key distribution process without being noticed.

• Bell’s theorem «reconciles» -under certain assumptions-the principles of locality and causality in quantum theory. It is a cornerstone result in modern physics.
• Locality states that no information can travel faster than light.
• Causality states that cause preceeds the effect.
• These two fundamental principles of nature were deemed incompatible by the famous Einstein-Podolsky-Rosen Paradox (EPR Paradox, 1935) in the framework of quantum theory.

---

References:

[1] Deloitte Touche Tohmatsu Limited: Tapping of Fibre Networks, (2017).

[2] Technical Information Bulletin 00-7v2: All-Optical Networks. NCS Technical Information Bulletin. US National Communications System, August 2020 – via Homeland Security Digital Library, USA.

[3] Zois, I.P.: Quantum Code Correction, National Military Centre for Research and Technology, Athens, Greece, Technical report No 211/1 (2012).

---

Recent Advances in MCDA

The key ingredient of Phoenix is MYRIAD, a tool suite developed by Thales for MCDA (Multi Criteria Decision Aiding) in Artificial Intelligence (AI).  Myriad in turn is based on  a two-additive Choquet Integral (see for example [1], [3], [4], [5]  & [6]). Motivated by the current coronavirus  pandemic and recognising the potential of MCDA, Dr Ioannis P. ZOIS suggested the idea to apply MCDA to speed up the trials for the covid 19 vaccine developed by his alma matter Oxford University and AstraZeneca Pharmaceuticals.  During 18-22 May 2020 the Bill and Melinda Gates Foundation organised a virtual conference with the general title «Artificial Intelligence in Drug and Vaccine Design and Testing». The conference was under the aegis of FDA (Food and Drug Administration, USA) and it was supported by CERN Computing (which helped with simulations), NASA, ESA, the Oak Ridge and Los Alamos National Labs in the US etc. The participants included some of the  top medical schools in the world (Oxford, Harvard, Cambridge etc ), some of the top pharmaceutical firms in the world (like Pfizer US, Glaxo UK, Sanofi France, Beyer Germany, Roche & Novartis Switzerland etc) along with defence industry (Locheed Martin, Dassault, British Aerospace, Boeing), computer companies (IBM, Microsoft, Intel) etc. Dr I. P. Zois  gave a talk entitled «Quantized calculus in MCDA and Deep Machine Learning» and he was also a member of the conference organising committee. The chairs of the conference were 3 world class scientists:

• Sir Peter J. Ratcliffe (Oxford University, Nobel prize medicine 2019),
• William G. Kaelin (Harvard University, Nobel prize medicine 2019) and
• Geoffrey Hinton (Cambridge & Toronto Universities, Turing Award 2018 for Deep machine learning and Artificial neural networks).

Dr Zois developed and presented an outline of an advanced version of MCDA based on state-of-the art pure mathematics like Quantized Calculus. QC  was developed fairly recently by two of the world most eminent mathematicians,  Alain Connes from IHES and College de France and Daniel Quillen from Oxford University, both Fields Medalists (both of whom have collaborated with Dr Zois in the past, see [2]).

The conference articles will appear in the New England Journal of Medicine (Conference Series, Impact factor 70.67), (printed version, see [7]).

---

References:

[1] Choquet, G.: «Theory of capacities”, Annales de l’Institut Fourier, 5: 131–295 (1953).

[2] Connes, A.: Noncommutative Geometry, 2nd Edition, Academic Press (2018).

[3] Denneberg, D.: Non-additive measure and Integral, Kluwer Academic (1998).

[4] Labreuche, C. and Fabien Le Huédé, F.: MYRIAD: a tool suite for MCDA, EUSFLAT Conf., pp. 204-209. (2005).

[5] Labreuche, C. and Fossier, S.: Explaining Multi-Criteria Decision Aiding (MCDA) Models with an Extended Shapley Value, IJCAI, pp. 331-339. (2018).

[6] Grabisch, M. and  Labreuche, C.: A decade of application of the Choquet and Sugeno integrals in multi-criteria decision aid (MCDA), Annals of Operations Research 175, no. 1 (2010): 247-286

[7] Zois, I.P., Rogers, T. and Hill, S.: «Generalised Non-additive measure theory, Choquet-Sougeno non-linear integration & Quantized Calculus in Deep Machine Learning and Multi Criteria Decision Aiding Algorithms: An example in the probabilistic assessment of hypercytokinemia from covid-19 viral vector vaccines» , New England Journal of Medicine Special issue Vol. I on Artificial Intelligence in Drug and Vaccine Design and Testing, Boston, MA, 2020.